Contents
What is card bunching?
Card bunching refers to the card removal effect caused by folding ranges. Simply put, players are more likely to muck low cards than high cards. This creates a bias - after several players fold we expect the deck and remaining players to hold slightly more high cards than low cards on average. The effect seems negigible at first, but it compounds quickly when multiple players fold consecutively. Conversely, when a player opens and another player calls, we expect the opposite effect. Since players are more likely to have opened/called higher cards, we expect the deck to generally contain lower cards. Although it comes down to the exact ranges in play.
It's important to note that this assumes randomly dealt hands with a fair deck. We're leveraging the information from players who've folded to gain insight about the deck distribution.
This effect is far-reaching. It impacts your expected value, your equity, the probability of hitting your outs, the runout frequencies postflop, the weighted probability of hand combinations in everyone's ranges, and of course, it impacts the optimal strategy. Unfortunately, most 2-player solvers completely ignore the bunching effect.
The significance of the bunching effect can range from negligible to very noticeable. Conventional wisdom in the poker community has been that card bunching is just a fringe effect that can be safely ignored. However, there is a general tendency to downplay effects that cannot be easily accounted for with standard tools.
Luckily, HRC supports full bunching using the Monte Carlo mode. We've recommended Monte Carlo mode to our users as the more accurate mode due to bunching for a while now, but we didn't thoroughly investigate how much EV is actually at play here. It's actually not that complicated, so let's take a closer look.
A quick visualization:
A picture is worth a thousand words. Let's say you're playing 9max, 100bb deep. It folds to you in the SB. If you open any two cards, you might expect your range to simply look like 100% of any two cards. However, because UTG-BTN were more likely to have mucked low cards, we expect to have high cards more often when the action plays out like this.
If we adjust the frequencies for how often you'd be dealt different hands, then opening any two cards would result in a range that looks something like this:
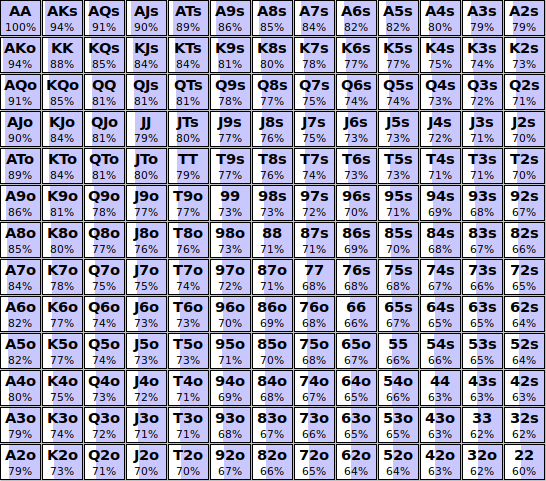
Put another way, applying this strategy to a (non-bunching) randomly dealt hand will result in the same relative hand frequencies as opening any two cards with bunching.
Now obviously, this will depend on the exact folding ranges in play. We'll dive further into the details of the above example shortly. But first, we need to refresh the basics.
Toy game example
Let's start with a simple toy game example.
- 3-handed, BU folds and we know that BU would have opened any hand containing an ace.
- At this point, what's the probability of SB holding an ace?
There are 4 aces in a 52 card deck. Therefore, The probability of SB drawing at least one ace from a random 52 card deck is given by (1 - (probability of not drawing an ace on the first card) * (probability of not drawing an ace on the second card)) or simply, 1 - (48/52 * 47/51) = 14.9%.
However, after the button folds, we know there are 4 aces left in the 50 unknown cards. The probability of SB holding at least one ace is now 1 - (46/50 * 45/49) = 15.5%
This effect compounds every time an additional player folds. We can imagine a 9-handed toy game where no one open-folds an ace in order to visualize how the effect builds up. After 7 players fold, the probability of SB holding at least one ace is 1 - (34/38 * 33/37) = 20.2%. In other words, they're now 35.3% more likely to have an ace!
The effect isn't quite as straightforward in actual games. Most players will not open any ace from any position, so the calculation becomes more complex.
We'll look at two more realistic examples:
- Scenario A: push-or-fold rakeless game with 7.5bb stacks and 10% antes. This scenario results in wide ranges that are very biased towards high cards. We expect this to be around the maximum bunching effect that we can see in actual game-play.
- Scenario B: 100bb, 10% ante, rakeless game. These ranges are a fair bit tighter than our first example and are less dominated by high cards. This should give us a more realistic idea about everyday bunching implications.
Scenario A: 7.5bb push-or-fold
- Push-or-Fold
- 9 player table
- 7.5bb stacks
- 0.1bb antes
- ChipEV
The standard no-bunching solution and its in-game EV
We can use the standard "Basic Hand" calculation mode in HRC as a starting point. This mode calculates EVs by enumerating over the player ranges across all board runouts. That's nice because it results in fully reproducible EVs and quick calculations, but this process ignores the bunching effect of folded ranges. This no-bunching solution is what you'll get from most ICM tools on the market.
NO-BUNCHING: Opening ranges, 9-max 7.5bb, 10% antes

Full ranges: 7.5bb no-bunching
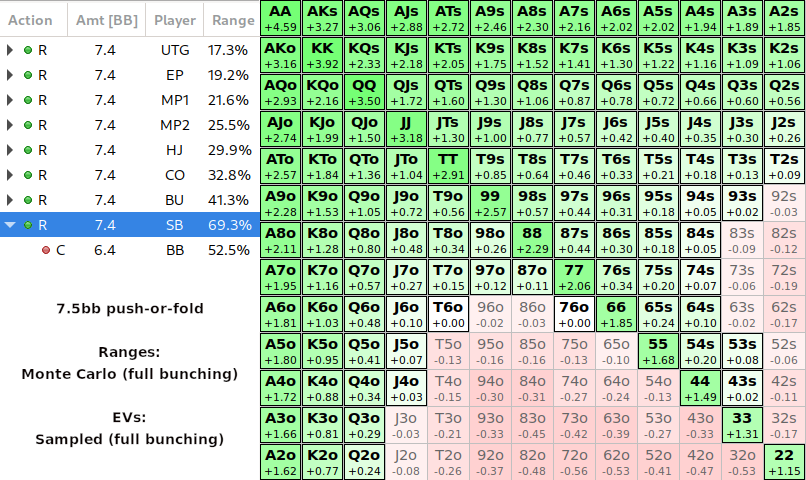
The EVs displayed for the solution above are calculated without considering bunching. When it folds to the SB, the solver still assumes a perfectly random deck. Let's examine how the folds from UTG to BU actually affect the EVs of SB's range. We simply copy the exact ranges from the enumerated solution into a Monte Carlo hand and let it simulate the EVs by random sampling.
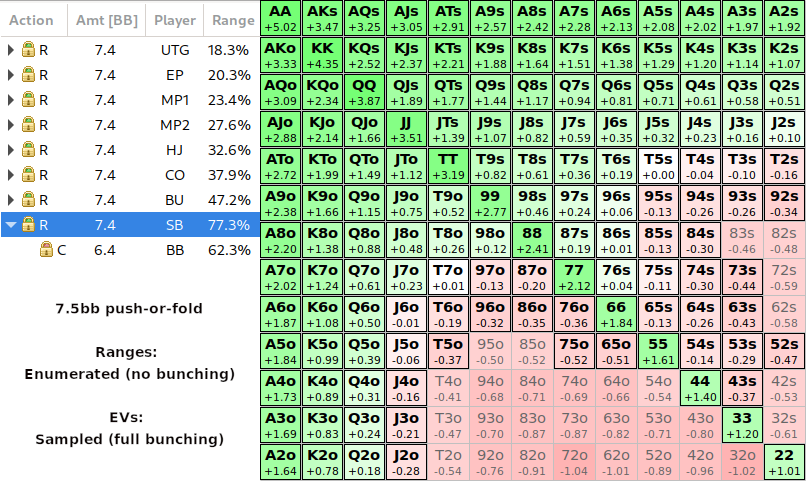
Let's remember what is displayed here: If everyone at the table is using the original no-bunching strategy (which is what most people who run non-bunching ICM sims are doing), this is what the actual in-game EV looks like. If you are using a tracker with all-in adjusted EVs, it will probably show you as running below EV for these shoves. That's because your tracker also assumes an unbiased shuffled deck when calculating the all-in EV.
We can observe some fairly sizable EV swings in there, especially towards the bottom of that range. Around 24% (approximately 18.3% / 77.3%) of the hand combinations in the original pushing range are unprofitable... In fact, some of the worst pushes (e.g. 75o) are losing as much as 0.5bb in EV (50 bb/100 mistake), which is about as bad as shoving 72o in the original no-bunching simulation!
Overall this is quite in line with what we expect to see:
- High Ax increase in value:
hitting boards more frequently
getting called more often by weaker Ax - Lower Ax are a mixed bag:
hitting boards more frequently
getting called more often by dominating Ax - Low connector type hands lose value:
getting called more often.
hitting boards less frequently - Pockets decrease in value:
more high cards on the board
Sanity checking the no-bunching solution in Monte Carlo mode
To demonstrate that this is not due to other differences between the two calculation modes, we can verify the EVs from the enumerated solution by running a Monte-Carlo simulation and nodelocking UTG-BTN ranges to 0%. This eliminates the card removal effects from the folds and should give us near-identical EVs to the original no-bunching results:

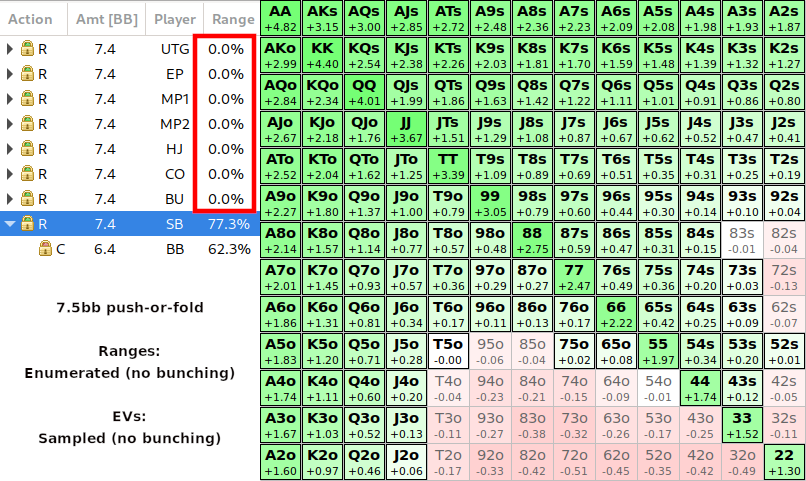
As we can see, everything works out, and the Monte Carlo mode produces almost precisely the same EVs as the Math mode in this case. Some minor differences are expected, as the EVs are now estimated by random sampling.
A quick look into 6-max
Let's see how things change for 6-max; we don't even have to set up a new calculation for this. Instead, simply lock the opening ranges of the first three positions to 0% and simulate again.

No big surprises here: We see similar EV shifts, just smaller. Considering that we moved from 7 folding ranges down to just 4, the effect is still remarkably significant.
The bunching adjusted solution
So what should our ranges look like if we account for the bunching effect?
All we have to do is run the same calculation in Monte Carlo mode, but this time without locking any of the ranges.
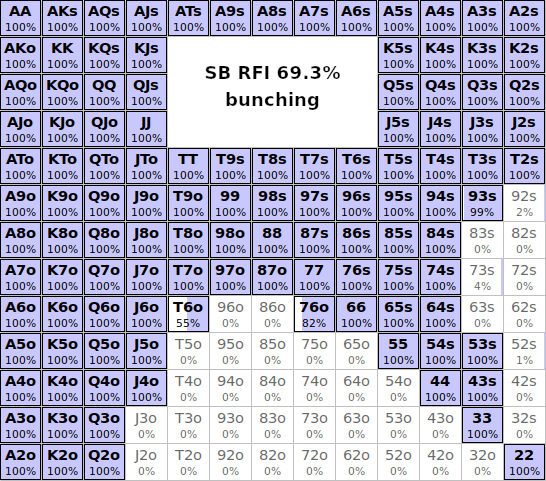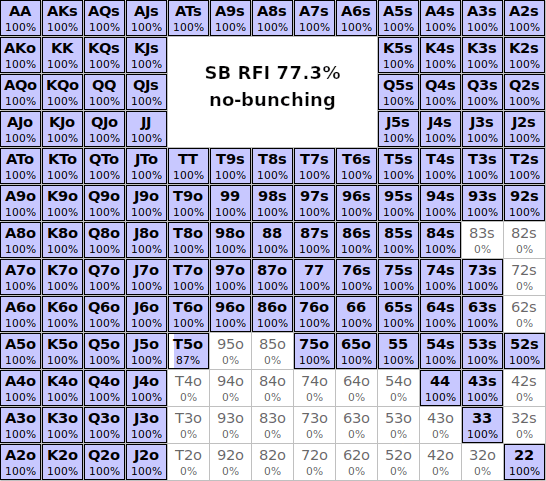
BUNCHING ADJUSTED: Opening ranges, 9-max 7.5bb, 10% antes
| Position | Bunching | Enumerated |
|---|---|---|
| UTG | 17.3% | 18.3% |
| EP | 19.2% | 20.3% |
| MP1 | 21.6% | 23.4% |
| MP2 | 25.5% | 27.6% |
| HJ | 29.9% | 32.6% |
| CO | 32.8% | 37.9% |
| BU | 41.3% | 47.2% |
| SB | 69.3% | 77.3% |
| SB vs BB | 52.5% | 62.3% |
Full ranges: 7.5bb bunching
The most glaring differences are the late position ranges: SB is shoving considerably tighter (69.3% vs 77.3%), even though BB defends a tighter range (52.5% vs 62.3%). While the range is tighter than the original no-bunching solution, it is significantly wider than the 59% of combos that were previously +EV in our simulation of the no-bunching ranges. That's because BB was also calling too wide in the earlier simulation, which made the wide pushes even worse.
A strategy comparison of the SB push:
Comparing the SB's EV between the non-bunching and bunching simulations

We see much smaller EV changes this time, compared to the earlier EV simulations. That's because of the tighter calling range of the BB in the bunching solution.
Why are the early position opening ranges different?
It's also worth noting that even the early position opening ranges are a notch tighter than in the no-bunching solution. Obviously, there are no bunching effects from open folds in play for the UTG opening range, so what's going on here?
The relevant bunching effects for this line are after UTG opens a hand: As the other players fold against that open, the distribution of the remaining cards also becomes slightly skewed towards higher cards. This increases the probability that one of the players behind will eventually have a calling hand, which means fewer successful steals compared to the enumerated solution. This effect is much less significant though; the calling ranges against an early position shove are very tight at around 6%, so the folding ranges still contain plenty of high cards.
Card distribution when folded to the SB
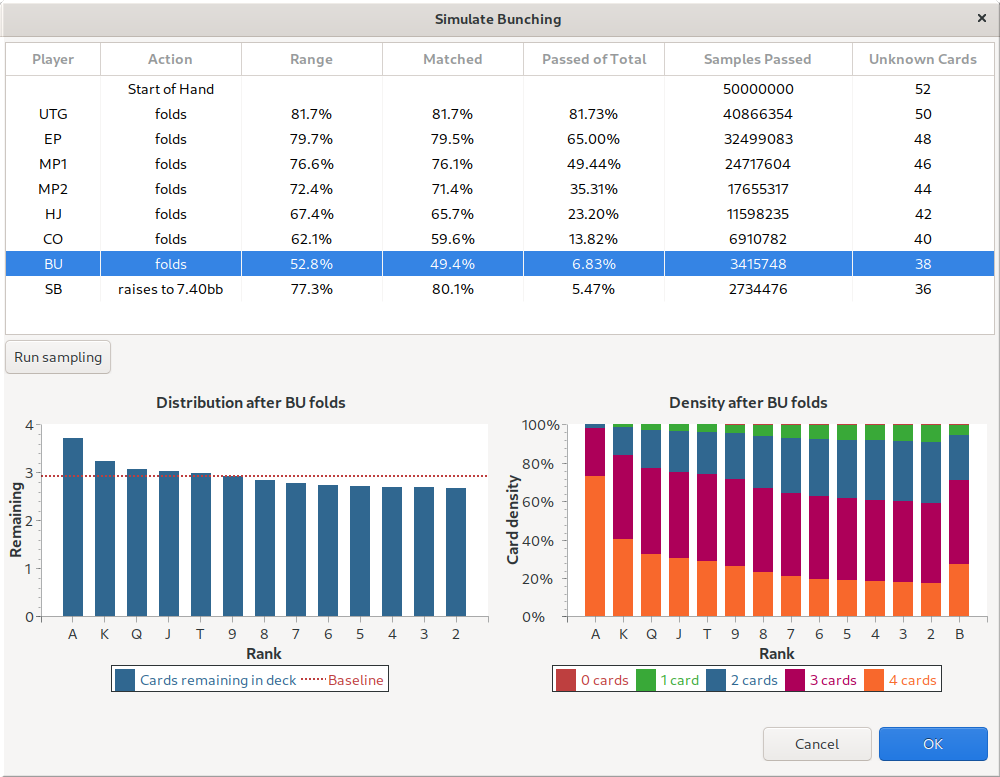
Solvers that ignore bunching implicitly assume that the remaining hole cards and the deck are still randomly distributed after several players fold. Let's see how much skew we can observe in the card distributions when folded to the SB.
For the 9-max games we have 7 players folding before action reaches the SB player, which means there are still 38 unfolded cards at this point. If those 7 players fold 100% of their dealt hands, we'd expect each rank to still make up 1/13th of the remaining 38 cards, for an average 38 / 13 = 2.92 occurrences per rank, or about a 7.7% density per card.
We can simulate the actual distribution by dealing random hands to all players. First, we test whether the action would be folded to the SB given the preflop ranges. If not, we throw out the sample. If so, we count the ranks with the remaining cards towards the simulated average.
Average remaining cards per rank when action folds to the SB:
| Rank | Avg. cards remaining | Change from baseline |
|---|---|---|
| A | 3.70 | +26.5% |
| K | 3.15 | +7.9% |
| Q | 3.04 | +4.1% |
| J | 3.03 | +3.7% |
| T | 2.98 | +2.0% |
| 9 | 2.91 | -0.4% |
| 8 | 2.80 | -4.3% |
| 7 | 2.78 | -5.0% |
| 6 | 2.75 | -6.0% |
| 5 | 2.73 | -6.7% |
| 4 | 2.73 | -6.8% |
| 3 | 2.71 | -7.4% |
| 2 | 2.70 | -7.6% |
| Aces | Kings | Queens | Jacks | Tens | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. cards remaining | 3.70 | 3.15 | 3.04 | 3.03 | 2.98 | 2.91 | 2.80 | 2.78 | 2.75 | 2.73 | 2.73 | 2.71 | 2.70 |
| Change from baseline | +26.5% | +7.9% | +4.1% | +3.7% | +2.0% | -0.4% | -4.3% | -5.0% | -6.0% | -6.7% | -6.8% | -7.4% | -7.6% |
On average, 3.7 aces remain out of 38 cards in the deck. In other words, the 14 folded cards contain an average of only 0.3 aces when action folds to the SB. Thus, aces occur 26.5% more frequently in these remaining 38 cards, compared to a regular shuffled deck and make up about 1/10th of cards instead of 1/13th. All broadway cards occur more frequently than in a random shuffle; however, the effect is much more pronounced for aces.
Alternatively, we can represent this card distrubtion as a graph:
Let's take this one step further by breaking down the probability of having 4, 3, 2, 1, or 0 of each card remaining in the deck. 72% of the time, we expect to see all four aces remaining. Compare that to the 18% that we expect all four 2's remaining. This gives us insight into how many outs we might expect with different hands, especially when setmining.
Now we can take all of this data and translate it into a familiar range matrix. Here's what a normalized range of any two cards looks like when accounting for the bunching effect:
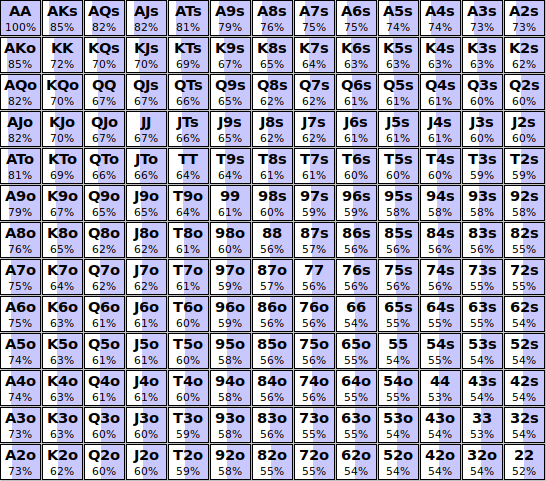
Okay wait a minute, if we're not dealt these hands at an even frequency, then wouldn't that change our preflop frequencies? If we are opening, for example, the top 50% of hands, do we actually end up playing 50% of the time? The answer is a resounding NO for the late positions.
| Position | Hole card combinations | Bunching adjusted frequency |
|---|---|---|
| UTG | 17.3% | 17.3% |
| EP | 19.2% | 19.4% |
| MP1 | 21.6% | 22.0% |
| MP2 | 25.5% | 26.4% |
| HJ | 29.9% | 31.6% |
| CO | 32.8% | 35.2% |
| BU | 41.3% | 44.5% |
| SB | 69.3% | 72.5% |
| BB vs SB | 52.5% | 56.1% |
Even though the BB is only defending 52.5% of hands against a SB push, they actually hold one of these combinations 56.1% of the time when the action plays out like this.
Scenario B: 100bb deepstacked
- 9 player table
- 100bb stacks
- 0.1bb antes
- ChipEV
- Opening 2.25bb, 3-bets to 8.5bb, 4-bets to 22bb
Examining the ranges
The second example uses 100bb opening ranges calculated using the latest postflop beta update. These are not meant to be definitive opening ranges by any means, but they should do just fine as an approximation of general opening range composition for game play with deeper stacks. Compared to the first scenario, we can see tighter ranges and less emphasis on high cards in the opening ranges, so we expect to see reduced bunching effects for this scenario.
Scenario B opening ranges, 9-max 100bb, rakeless, 10% antes
| Position | Opening hole card combinations | Bunching adjusted frequency |
|---|---|---|
| UTG | 14.2% | 14.2% |
| EP | 15.9% | 16.0% |
| MP1 | 18.7% | 19.0% |
| MP2 | 22.1% | 22.6% |
| HJ | 27.4% | 28.2% |
| CO | 35.5% | 36.9% |
| BU | 54.8% | 57.0% |
For example, BU opens 54.8% of hands. But when it is folded to the BU, they actually hold one of these hands 57.0% of the time.
Full ranges: 100bb
Card distribution when folded to the SB
Just as before, let's graph the deck density when it has folded to us in the SB:
| Rank | Avg. cards remaining | Change from baseline |
|---|---|---|
| A | 3.41 | +16.5% |
| K | 3.19 | +9.2% |
| Q | 3.08 | +5.3% |
| J | 3.04 | +4.0% |
| T | 3.03 | +3.6% |
| 9 | 2.92 | -0.2% |
| 8 | 2.88 | -1.5% |
| 7 | 2.83 | -3.2% |
| 6 | 2.78 | -5.1% |
| 5 | 2.79 | -4.7% |
| 4 | 2.72 | -6.8% |
| 3 | 2.69 | -8.0% |
| 2 | 2.66 | -9.1% |
| Aces | Kings | Queens | Jacks | Tens | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. cards remaining | 3.41 | 3.19 | 3.08 | 3.04 | 3.03 | 2.92 | 2.88 | 2.83 | 2.78 | 2.79 | 2.72 | 2.69 | 2.66 |
| Change from baseline | +16.5% | +9.2% | +5.3% | +4.0% | +3.6% | -0.2% | -1.5% | -3.2% | -5.1% | -4.7% | -6.8% | -8.0% | -9.1% |
As expected, the bunching effect is less pronounced than the push-fold solution, but still quite significant!
Now let's examine a detailed breakdown of how many of each card we expect in the deck when it folds to the SB:
Lastly, let's put this data into a format we're all familiar with. Here's the SB opening range with any two cards, adjusted for the bunching effect:

Clearly bunching is still quite significant in 100bb deepstacked situations.
Conclusions
Bunching has an impact on everything from your EV to your strategy to your frequencies. It affects cash game and tournament players alike, affecting both chipEV and ICM-EV. In general, bunching increases the value and frequency of high cards, and decreases the value and frequency of low cards. Bunching ranges tend to be tighter than non-bunching ranges.
Most solvers completely ignore this effect, implicitly believing that they're drawing from an even deck. However, the card removal from folded ranges can skew the deck probabilities.
Our most important takeaway is that bunching certainly has a pretty sizable effect on EVs - especially accentuated in short stack scenarios - and easily has the potential to swing profitable opens into clear mistakes. The effect is actually considerably larger than we expected and we'd like to encourage our more experienced HRC users to switch to the Monte Carlo engine as their default calculation mode, even for push-or-fold calculations. This mode may be a bit harder to use, but we think the added accuracy makes it worthwhile.
We'd also like to assist players with incorporating bunching into their decision-making process. We've started by integrating bunching-related tools into the HRC beta, this option is available as "Node Details" in the context menu of ranges. Initially, this includes bunching-related plots similar to the ones in this post, so users can easily visualize the card distribution at any point of a hand.