2018-06 HRC Update: KO/PKO Bounty Tournaments

Overview

This is a fairly big content update, some of the features have been available for beta testing for almost two years.

Here is a quick overview of the main changes included in this update:

• Support for KO/PKO calculations for all $EV models
• Support for raked cash games
• Equities for $EV models are now displayed as % of table equity by default
• Option to increase the blind level within the scope of FGS calculations
• Option to export the range grid table to HTML
• The full list of changes is available in the Changelog

As these features move into the stable release, we're about to start a new cycle of beta features later this month. Please check back for announcements in our News, the upcoming beta version will require a separate installation and won't be rolled out via the automatic update system.

Changed display for $EV models

We changed the default equity display for $EV models to better suit bounty calculations and calculations for large MTT fields. This change does not affect calculated ranges, just the absolute size of the +/- EQDiff% values.

Equities are now displayed as percentage of the total $EV on the calculated table. For single table calculations this is equal to the sum of all remaining regular prizes and bounties. For multi-table calculations the equities are normalized so the sum of all EQPre% values on the active table equals 100%.

For hands where the new equity display is different than the traditional one, e.g. calculations with bounties and/or MTT, the conversion factor to the old mode can be displayed by hovering the mouse over the header of the hand tab.

If you prefer to keep the old equity display, as % of total regular prizes, you can revert back to this mode at Window: Preferences: Equity Display.

Bounty SNG/MTT support

The main addition in the new version is support for the popular knockout / bounty formats. Bounty support is available for all $EV models (ICM/FGS/MTT).

The setup for bounty calculation differs by type:

• Regular KO: The bounty on every player remains equal for the entire tournament and the full bounty amount is paid out immediately on elimination.
• Progressive KO: Bounties may vary between players and on elimination 50% of the bounty amount is paid out and the remaining 50% is added to the eliminating player's bounty.

Setup of regular KOs

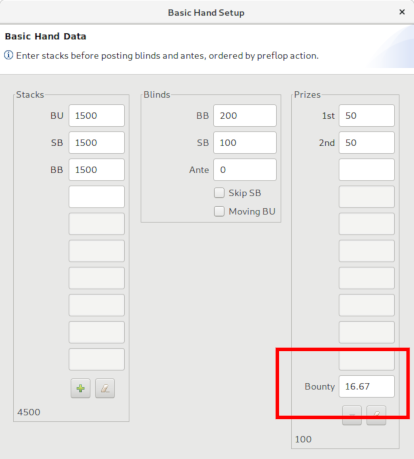
Regular KO calculations use the Bounty setting below the regular prize setup, this setting defines the bounty amount per player. It is important that the bounty setting is in the correct relation to the regular prizes. The simplest solution is to enter both regular prizes and bounties in $.

On the following bounty configuration page, select "Keep bounty configuration", this additional dialog page is only relevant for PKO calculations where bounties vary by player.

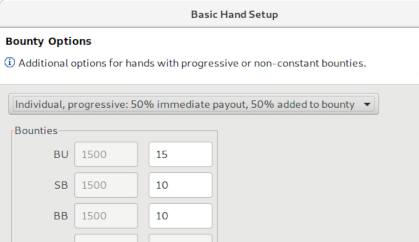
Setup of progressive KOs

Progressive KO calculations do not use the bounty setting mentioned before, instead the bounty amount for each player is defined individually on a separate dialog page. As with regular KO calculations, it is important that bounties are entered in correct relation to the regular prizes, preferably enter everything in $. The individual bounties are imported automatically from the hand history for PokerStars PKOs.

For MTT PKO calculations only bounties on the active table are entered. For other tables the calculation assumes that the average bounty per player is the same as the average on the active table. This should be reasonably accurate in most situations, but we may add an additional setting at a later time to allow overriding of this assumption.

Typical PKO tournaments distribute 50% of a player's bounty immediately on elimination and add the remaining 50% to the eliminating player's bounty. There is an alternative setting that allows individual bounties but distributes the full amount on elimination. This is useful for the calculation of special game modes, such as Party Poker's Sit & Go HERO.

Bounty calculation details

Knockout support is composed of two parts:

1. Awarding bounties for knockouts that occur within the calculation scope. This part is a direct application of the KO/PKO tournament rules. If a player is eliminated within the scope of the calculation, the corresponding bounty is added to the tournament equity of the eliminating player.
2. In addition, the calculation also estimates the additional $ equity from bounties that will be awarded later in the tournament. We use proportional estimates for remaining bounties, e.g. a player holding 10% of the chips in play is expected to capture 10% of the remaining bounties. These bounty estimates are then added to the equity estimates for the regular prize pool to calculate the overall tournament equity.

This second part of the calculation is naturally only a projection. There were initially several other bounty models included for beta testing (flat, moderate, proportional), but after extensive evaluation the stable version will only include the proportional model. The proportional model is by far the easiest to understand and based on our testing it also offers the most accurate estimates, so we decided to keep things simple. A summary about our evaluation of bounty models will be publicly available on this site at a later time.

What about ChipEV bounty calculations?

We are aware that some players use ChipEV approximations to calculate bounties, by converting the $ amount of bounties into additional chips that are added as overlay into the pot. Bounties can only be used with the $EV models in HRC and we have no plans to integrate bounties into ChipEV calculations. ChipEV deals strictly with chips and supporting $ bounties in ChipEV calculations would introduce an inconsistent mix.

These ChipEV bounty approximations are mostly used for the beginning stages of tournaments, where ICM considerations are often negligible and setting up the prize structure for large field tournaments can be tedious. However, it is easy to run bounty calculations without ICM considerations in a more consistent manner, within the normal $EV framework.

Example: Setting up early stage MTT calculations

To quickly setup bounty calculations for the early stages of MTTs, without ICM considerations, simply set the structure for regular prizes to be winner-takes-all and generate the the correct number of players and chip totals.

As an example, let's set up the first hand of the following tournament:

• Regular KO MTT 9$ + 3$, each buy-in contributes 9$ to regular prizes and 3$ as bounty
• 500 players total

Steps:

1. Enter the stacks and blinds for the active table as usual
2. Select MTT ICM as equity model and switch to the MTT dialog page
3. Enter the total regular prize pool (500 * 9$ = 4500$) as first prize
4. Set bounties to 3$
5. Generate the remaining stacks, 500 total, with an average of the starting stack

That's it, this calculation closely resembles the popular ChipEV approximations.